Product: Abaqus/Explicit
This verification test consists of a list of single-element models that use either C3D8R or CPE4R elements and are run under simple loading conditions (uniaxial tension, uniaxial compression, and simple shear). The purpose of this example is to test the equation of state material model and its combination with the Mises and Johnson-Cook plasticity models. Two parallel sets of models are studied. The first set uses the linear elastic, linear elastic with Mises plastic, and linear elastic with Johnson-Cook plastic materials. The second set uses the linear 
type of EOS, linear type of EOS with Mises plastic, and linear type of EOS with Johnson-Cook plastic materials.
For linear elasticity the volumetric response is defined by
Hugoniot form is
is the same as the nominal volumetric strain measure, 
. Thus, setting the parameters 
0.0 and 
0.0 gives the simple hydrostatic bulk response, which is identical to the elastic volumetric response. The elastic deviatoric response of the material is defined by the shear modulus. The elastic material properties are Young's modulus = 207 GPa and Poisson's ratio = 0.29. The initial material density, 
, is 7890 kg/m3. The equivalent properties for the linear type of equation of state material model are 
= 4563.115 m/s and shear modulus = 80.233 GPa. For models in which plasticity (including both Mises and Johnson-Cook plasticity models) is used, the plastic hardening is chosen to be
is the yield stress (in units of MPa) and 
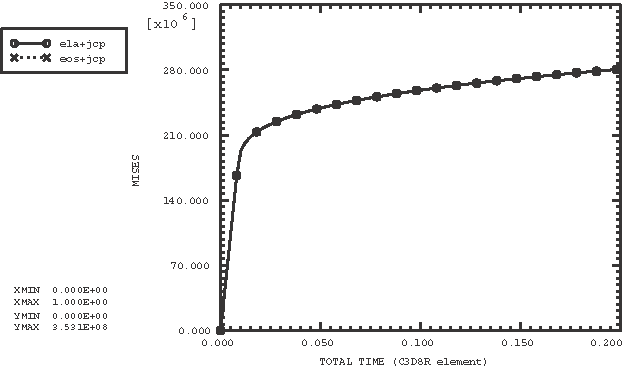
is the equivalent plastic strain.The results obtained from the analyses that use the EOS material model match the corresponding results obtained from the analyses that use the linear elasticity model. The comparison of the pressure and Mises stresses obtained with the EOS material model (with Johnson-Cook plastic shear response) and the linear elasticity model (with the same Johnson-Cook plastic shear response) using the C3D8R element under uniaxial tension loading are shown in Figure 2.2.20–1 and Figure 2.2.20–2, respectively. The uniaxial compression comparisons are shown in Figure 2.2.20–3 and Figure 2.2.20–4.
Uniaxial tension test.
Uniaxial compression test.
Simple shear test.
Simple shear test with nonzero initial conditions for .
Figure 2.2.20–1 Pressure stress in uniaxial tension: elastic response versus linear type of equation of state response.
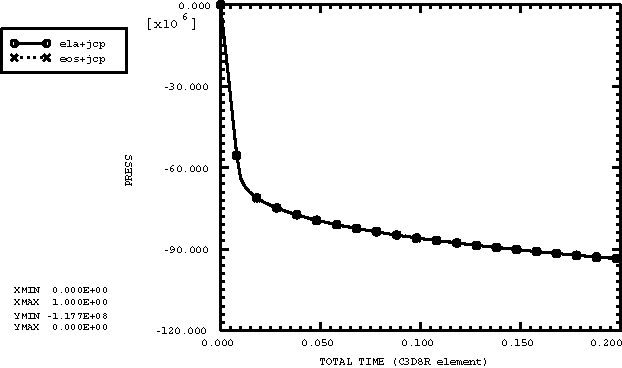
Figure 2.2.20–2 Mises stress in uniaxial tension: elastic response versus linear type of equation of state response.
This verification test consists of single-element models that use either C3D8R or CPE4R elements and are run under simple loading conditions (uniaxial tension, uniaxial compression, and simple shear). The purpose of this example is to test the tabulated EOS material model and its combination with the Mises and Johnson-Cook plasticity models. Two parallel sets of models are studied. The first set uses the linear elasticity, linear elasticity with Mises plasticity, and linear elasticity with Johnson-Cook plasticity materials. The second set uses the tabulated EOS, tabulated EOS with Mises plasticity, and tabulated EOS with Johnson-Cook plasticity materials.
For linear elasticity the volumetric response is defined by
and 
are functions of the logarithmic volumetric strain 
only, with 
, and 
is the reference density. Thus, setting the functions 
and 
0.0 gives the simple hydrostatic bulk response, which is identical to the elastic volumetric response. The elastic deviatoric response of the material is defined by the shear modulus.The elastic material properties are Young's modulus = 207 GPa and Poisson's ratio = 0.29. The initial material density, , is 7890 kg/m3. The properties for the tabular EOS material model are computed using 
= 164.286 GPa and shear modulus = 80.233 GPa. For models in which plasticity (including both Mises and Johnson-Cook plasticity models) is used, the plastic hardening is chosen to be
is the yield stress (in units of MPa) and is the equivalent plastic strain.The results obtained from the analyses that use the EOS material model match the corresponding results obtained from the analyses that use the linear elasticity model.
Uniaxial tension test.
Uniaxial compression test.
Simple shear test.
Simple shear test with nonzero initial conditions for .
This verification test consists of single-element models that use either C3D8R or CPE4R elements and are run under simple loading conditions (uniaxial, hydrostatic, and simple shear). The purpose of this example is to test the 
equation of state material model and its combination with different models for the deviatoric behavior: linear elastic, Newtonian viscous shear, and Mises and Johnson-Cook plasticity; as well as itscombination with different models for the hydrodynamic response of the solid phase: Mie-Grüneisen and tabulated equations of state.
The material properties used for the tests are representative of partially saturated sand. They are summarized below:
Material:
Solid phase
Plasticity
For models with plastic shear behavior (either Mises or Johnson-Cook plasticity), the plastic hardening is chosen to be
is the yield stress (in units of MPa) and is the equivalent plastic strain. The plasticity models are used in combination with linear elastic shear behavior.The results obtained from the analyses agree well with exact analytical or approximate solutions. The evolution of the distension 
with hydrostatic pressure during a cyclic volumetric test is shown in Figure 2.2.20–5.
Uniaxial test.
Cyclic hydrostatic test.
Simple shear test.
Simple shear test with nonzero initial conditions for .
This verification test consists of single-element models that use either C3D8R or CPE4R elements and are run under simple shear loading conditions. The purpose of this example is to test the different viscosity models for both Newtonian and non-Newtonian fluids. The hydrodynamic response of the material is described by the Mie-Grüneisen equation of state in all cases. Some tests include thermo-rheologically simple temperature-dependent viscosity using the Arrhenius form.
The material properties used for the tests are summarized below:
Material:
Hydrodynamic properties
Viscous properties
The properties for each of the tested viscosity models are given below:
Mat8:
The results obtained from the analyses agree well with exact analytical or approximate solutions.
Simple shear test.
Material with Arrhenius TRS properties. Simple shear test.
User subroutine VUVISCOSITY for the user-defined Cross viscosity model used in eosshrvisc.inp and eosshrvisctrs.inp.
Equation of state (EOS) material model with pressure-dependent (Drucker-Prager) shear plasticity.
This verification test consists of single-element models that use either C3D8R, CPE4R, or CAX4R elements and are run under simple loading conditions (uniaxial tension, uniaxial compression, and simple shear). The purpose of this example is to test the combination of EOS models for the volumetric response of the material with the extended Drucker-Prager pressure-dependent plasticity models for the shear response. Some of the models also include Johnson-Cook strain-rate dependence in the plasticity definition.
Uniaxial tension test, Johnson-Cook strain-rate dependence, Drucker-Prager plasticity with exponent form shear criterion, C3D8R element.
Uniaxial tension test, Johnson-Cook strain-rate dependence, Drucker-Prager plasticity with exponent form shear criterion, CPE4R element.
Uniaxial tension test, Johnson-Cook strain-rate dependence, Drucker-Prager plasticity with exponent form shear criterion, CAX4R element.
Uniaxial tension test, Johnson-Cook strain-rate dependence, Drucker-Prager plasticity with hyperbolic shear criterion, C3D8R element.
Uniaxial tension test, Johnson-Cook strain-rate dependence, Drucker-Prager plasticity with hyperbolic shear criterion, CPE4R element.
Uniaxial tension test, Johnson-Cook strain-rate dependence, Drucker-Prager plasticity with hyperbolic shear criterion, CAX4R element.
Uniaxial tension test, C3D8R and CPE4R elements.
Uniaxial compression test, C3D8R and CPE4R elements.
Simple shear test, C3D8R and CPE4R elements.
This verification test consists of single-element models that use either C3D8R or CPE4R elements and are run under simple loading conditions (uniaxial tension, uniaxial compression, and simple shear). The purpose of this example is to test the user-defined EOS material model (user subroutine VUEOS) and its combination with the Mises and Johnson-Cook plasticity models. Two parallel sets of models are studied. The first set uses the linear elasticity, linear elasticity with Mises plasticity, and linear elasticity with Johnson-Cook plasticity materials. The second set uses the user-defined EOS, user-defined EOS with Mises plasticity, and user-defined EOS with Johnson-Cook plasticity materials.
For linear elasticity the volumetric response is defined by
is the reference density. The user subroutine needs to return the derivative of pressure with respect to density, 
, which is needed for the the evaluation of the effective moduli of the material that enters the stable time calculation. User subroutine VUEOS also returns the derivative of pressure with respect to the energy, 
, which is usually needed to solve the nonlinear pressure-energy dependency using the Newton method. In the case considered here, these quantities are
The elastic material properties are Young's modulus = 207 GPa and Poisson's ratio = 0.29. The initial material density, , is 7890 kg/m3. The properties for the tabular EOS material model are computed using = 164.286 GPa and shear modulus = 80.233 GPa. For models in which plasticity is used (including both Mises and Johnson-Cook plasticity models), the plastic hardening is chosen to be
is the yield stress (in units of MPa) and is the equivalent plastic strain.The results obtained from the analyses that use the EOS material model match the corresponding results obtained from the analyses that use the linear elasticity model.
Uniaxial tension test.
Uniaxial compression test.
Simple shear test.
Simple shear test with nonzero initial conditions for .
User subroutine VUEOS used in the input files listed above.
(
)
(sec-1)
