The simplest approach for combining design responses is to create an objective function with a weighted sum of design responses. Alternatively, you can combine design responses using the design response editor. You should be careful how you combine design responses to avoid creating a meaningless optimization task. In addition, you should understand how condition-based and general optimization combine terms and how they differ. The following topics are covered:
“Combining design responses for a condition-based topology or shape optimization
“Combining design responses for a general topology optimization
“Applying a cutoff filter to a design response for a shape optimization
For both condition-based topology and shape optimization the following methods are available for combining up to four design responses (
, 
, 
, and 
):
For both condition-based topology and shape optimization the following methods are available for combining two design responses ( and ):
For both condition-based topology and shape optimization the following methods are available for operating on a single design response:
| Absolute value |  |
| Sine |  |
| Cosine |  |
| Tangent |  |
| Common logarithm |  |
| Natural logarithm |  |
| Square root |  |
| Exponential |  |
| Nth Root |  |
| Nth Power |  |
| Integer |  |
| Nearest integer number |  |
| Sign |  |
 , the difference between two iterations |  |
For a general topology optimization you can create a design response that is calculated as the absolute difference between two design responses of the same type or a weighted combination of several (up to 10) displacement design responses. A typical example uses the absolute difference in the displacement between two design responses to constrain the displacement of two vertices relative to each other. The following table shows which design responses can be combined:
| Design responses | Absolute difference | Weighted sum |
|---|---|---|
| Displacements and rotation |  | |
| Absolute displacements and rotations | ||
| Reaction forces | | |
| Absolute reaction forces | ||
| Internal forces | | |
| Absolute internal forces | ||
| Modal eigenfrequencies | |
Although a design response is a single scalar value, you can use the appropriate weighting to combine design responses that are defined in different directions or in different coordinate systems.
You can apply a filter to a design response that will smooth out local peaks for a shape optimization. The filter is defined as
is the filter function for node j. The main filter function, 
, decreases with the distance, d, between nodes i and j. The maximum radius of influence, 
, defines the maximum distance from node j for the nodes i to influence the filter value. The local curvature, 
, is approximated by the vector product of the node normal, 
, and the neighboring nodes, 
. The curvature dependency, 
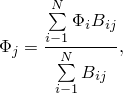
, defines a weight function that reduces the radius at higher local curvature.You can specify the following:
The maximum radius of influence, .
The exponent, p, which defines the weight function that controls the influence of the distance between nodes i and j. The default value is 1.0.
The surface bending radius reduction, 
. The default value of is 0.2. A larger value of decreases the influence of the surface curvature.
You can apply a filter that cuts off local peaks of the design response for a shape optimization. You can specify the following:
The lower bound of the design response. All values less than this lower bound are assumed to be zero.
The upper bound of the design response. All values greater than this upper bound are assumed to be the value of the upper bound.
You can normalize the vectors used as terms for the algorithm that calculates a shape optimization. You may want to normalize design responses before you combine them using a weighted combination; for example, if different loads are applied to different regions. If desired, you can apply either of the following nomalizations:
A normalization based on the maximum value in each design cycle (in effect, a normalization of 1.0 for each cycle).
A normalization based on the initial value of the design response (the maximum value during the first design cycle).
