The above procedure continues using this new list to define additional degrees of freedom in accordance with the new node and degrees of freedom. For example, consider a 3-node beam that has degrees of freedom 1, 2, and 6 at nodes 1 and 3 and degrees of freedom 1 and 2 at node 2 (middle node). To order degrees of freedom 1 first, followed by 2, followed by 6, the following input could be used:

*USER ELEMENT
1
1, 2
1, 6
2,
3, 6

There are the following additional requirements with respect to activated degrees of freedom on a user element of type VUn:

• Only degrees of freedom 1 through 6, 8, and 11 can be activated because these are the only degrees of freedom numbers that can be updated in Abaqus/Explicit. (In Abaqus/Standard degrees of freedom 1 through 30 can be used.)

• If one translational degree of freedom is activated at a node, all translational degrees of freedom up to the specified maximum number of coordinates must be activated at that node; moreover, the translational degrees of freedom at the node must be in consecutive order.

• In three-dimensional analyses, if one rotational degree of freedom is activated at a node, all three rotational degrees of freedom must be activated in consecutive order.

*USER ELEMENT
1,2,3,4,5,6
2,11
3,1,2,3,11
4,1,2,3,4,5,6

If all three rotational degrees of freedom (4, 5, and 6) are used at a node in a geometrically nonlinear analysis, Abaqus assumes that these rotations are finite rotations. In this case the incremental values of these degrees of freedom are not simply added to the total values: the quaternion update formulae are used instead. Similarly, the corrections are not simply added to the incremental values. The update procedure is described in “Rotation variables,” Section 1.3.1 of the Abaqus Theory Guide, and is mentioned in “Conventions,” Section 1.2.2.

To avoid the rotation update in a geometrically nonlinear analysis in Abaqus/Standard, you may define repeated node numbers in the nodal connectivity of the element such that at least one of the degrees of freedom 4, 5, or 6 is missing from the degree of freedom list at each node.

To read the element matrices from an Abaqus/Standard results file, you must have written the stiffness and/or mass matrices in a previous analysis to the results file as element matrix output (“Element matrix output in Abaqus/Standard” in “Output,” Section 4.1.1) or substructure matrix output (“Writing the recovery matrix, reduced stiffness matrix, mass matrix, load case vectors, and gravity vectors to a file” in “Defining substructures,” Section 10.1.2).

You must specify the element number, n, or substructure identifier, Zn, to which the matrices correspond. For models defined in terms of an assembly of part instances (“Defining an assembly,” Section 2.10.1), the element numbers written to the results file are internal numbers generated by Abaqus/Standard (see “Output,” Section 4.1.1). A map between these internal numbers and the original element numbers and part instance names is provided in the data file of the analysis from which the element matrix output was written.

In addition, for element matrix output you must specify the step number and increment number at which the element matrix was written. These items are not required if a substructure whose matrix was output during its generation is used.

*USER ELEMENT, FILE=name, OLD ELEMENT=n or Zn, STEP=n, INCREMENT=n

If you define the stiffness and/or mass matrix directly, you must specify the number of nodes associated with the element.

*USER ELEMENT, LINEAR, NODES=n

*USER ELEMENT, LINEAR, NODES=n, UNSYMM

*MATRIX, TYPE=MASS

*MATRIX, TYPE=STIFFNESS

*MATRIX, TYPE=MASS or STIFFNESS, INPUT=file_name

  
   
    
     
     
  
     
   
Etc.

     
     
…
…,   
     
Etc.

You must associate a property definition with every user element, even though no property values (except Rayleigh damping factors) are associated with linear user elements.

*UEL PROPERTY, ELSET=name

Defining Rayleigh damping for direct-integration dynamic analysis

You can define the Rayleigh damping factors for direct-integration dynamic analysis (“Implicit dynamic analysis using direct integration,” Section 6.3.2) for linear user elements. The Rayleigh damping factors are defined as

where is the damping matrix, is the mass matrix, is the stiffness matrix, and and are the user-specified damping factors. See “Material damping,” Section 26.1.1, for more information on Rayleigh damping.

Input File Usage:

*UEL PROPERTY, ELSET=name, ALPHA=, BETA=

You can apply point loads, moments, fluxes, etc.  to the nodes of linear user-defined elements in the usual way using concentrated loads and concentrated fluxes (“Concentrated loads,” Section 34.4.2, and “Thermal loads,” Section 34.4.4).

Distributed loads and fluxes cannot be defined for linear user-defined elements.

You must specify the number of nodes associated with a general user element. You can define “internal” nodes that are not connected to other elements.

*USER ELEMENT, NODES=n

If the contribution of the element to the Jacobian operator matrix of the overall Newton method is not symmetric (i.e., the element matrices are not symmetric), you can request that Abaqus/Standard use its nonsymmetric equation solution capability (see “Defining an analysis,” Section 6.1.2).

*USER ELEMENT, NODES=n, UNSYMM

You can define the maximum number of coordinates needed in user subroutines UEL, UELMAT, or VUEL at any node point of the element. Abaqus assigns space to store this many coordinate values at all of the nodes associated with elements of this type. The default maximum number of coordinates at each node is 1.

Abaqus will change the maximum number of coordinates to be the maximum of the user-specified value or the value of the largest active degree of freedom of the user element that is less than or equal to 3. For example, if you specify a maximum number of coordinates of 1 and the active degrees of freedom of the user element are 2, 3, and 6, the maximum number of coordinates will be changed to 3. If you specify a maximum number of coordinates of 2 and the active degrees of freedom of the user element are 11 and 12, the maximum number of coordinates will remain as 2.

*USER ELEMENT, COORDINATES=n

You can define the number of properties associated with a particular user element and then specify their numerical values.

*USER ELEMENT, I PROPERTIES=n, PROPERTIES=m

*UEL PROPERTY, ELSET=name

*UEL PROPERTY, MATERIAL=name

*UEL PROPERTY, ORIENTATION=name

*USER ELEMENT, TENSOR=THREED

*USER ELEMENT, TENSOR=TWOD

*USER ELEMENT, TENSOR=PSTRAIN

*USER ELEMENT, TENSOR=PSTRESS

*USER ELEMENT, INTEGRATION=n

You can define the number of solution-dependent state variables that must be stored within a general user element. The default number of variables is 1.

Examples of such variables are strains, stresses, section forces, and other state variables (for example, hardening measures in plasticity models) used in the calculations within the element. These variables allow quite general nonlinear kinematic and material behavior to be modeled. These solution-dependent state variables must be calculated and updated in user subroutines UEL, UELMAT, and VUEL.

As an example, suppose the element has four numerical integration points, at each of which you wish to store strain, stress, inelastic strain, and a scalar hardening variable to define the material state. Assume that the element is a three-dimensional solid, so that there are six components of stress and strain at each integration point. Then, the number of solution-dependent variables associated with each such element is 4 × (6 × 3 + 1) = 76.

*USER ELEMENT, VARIABLES=n

For a general user element in Abaqus/Standard, user subroutine UEL may be coded to define the contribution of the element to the model. Abaqus/Standard calls this routine each time any information about a user-defined element is needed. At each such call Abaqus/Standard provides the values of the nodal coordinates and of all solution-dependent nodal variables (displacements, incremental displacements, velocities, accelerations, etc.) at all degrees of freedom associated with the element, as well as values, at the beginning of the current increment, of the solution-dependent state variables associated with the element. Abaqus/Standard also provides the values of all user-defined properties associated with this element and a control flag array indicating what functions the user subroutine must perform. Depending on this set of control flags, the subroutine must define the contribution of the element to the residual vector, define the contribution of the element to the Jacobian (stiffness) matrix, update the solution-dependent state variables associated with the element, form the mass matrix, and so on. Often, several of these functions must be performed in a single call to the routine.

The element's principal contribution to the model during general analysis steps is that it provides nodal forces that depend on the values of the nodal variables and on the solution-dependent state variables within the element:

In general procedures Abaqus/Standard solves the overall system of equations by Newton's method:

Solve	,
Set	,
Iterate

During such iterations you must define , which is the element's contribution to the residual, , and

Use in transient analysis procedures

In procedures such as transient heat transfer and dynamic analysis, the problem also involves time integration of rates of change of the nodal degrees of freedom. The time integration schemes used by Abaqus/Standard for the various procedures are described in more detail in the Abaqus Theory Guide. For example, in transient heat transfer analysis, the backward difference method is used:

Therefore, if depends on and (as would be the case if the user element includes thermal energy storage), the Jacobian contribution should include the term

where is defined from the time integration procedure as .

In all cases where Abaqus/Standard integrates first-order problems in time, the are never stored because they are readily available as , where . However, for direct, implicit integration of dynamic systems (see “Implicit dynamic analysis,” Section 2.4.1 of the Abaqus Theory Guide) Abaqus/Standard requires storage of and . These values are, therefore, passed into subroutine UEL. If the user element contains effects that depend on these time derivatives (damping and inertial effects), its Jacobian contribution will include

For the Hilber-Hughes-Taylor scheme

where and are the (Newmark) parameters of the integration scheme. For backwark Euler time integration, the same expressions apply with and equal to unity. The term is the element's damping matrix, and is its mass matrix.

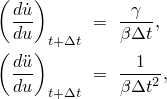
The Hilber-Hughes-Taylor scheme writes the overall dynamic equilibrium equations as

where is the total force at degree of freedom N, excluding d'Alembert (inertia) forces. is often referred to as the “static residual.” Therefore, if a user element is to be used with Hilber-Hughes-Taylor time integration, the element's contribution to the overall residual must be formulated in the same way. Since Abaqus/Standard provides information only at the time point at which UEL is called, this implies that each time UEL is called the array must be used to recover (and if half-increment residual calculations are required, where indicates from the beginning of the previous increment) and used to store (and if half-increment residual calculations are required) for use in the next increment. This complication can be avoided if the numerical damping control parameter, , for the dynamic step is set to zero; i.e., if the trapezoidal rule is used for integration of the dynamic equations (see “Implicit dynamic analysis using direct integration,” Section 6.3.2, for details). This complication is also avoided with the backward Euler time integration operator because dynamic equilibrium is enforced at the end of the step.

If solution-dependent state variables () are used in the element, a suitable time integration method must be coded into subroutine UEL for these variables. Any of the associated with the element that are not shared with standard Abaqus/Standard elements may be integrated in time by any suitable technique. If, in such cases, it is necessary to store values of , , etc. at particular points in time, the solution-dependent state variable array, , can be used for this purpose. Abaqus/Standard will still compute and store values of and using the formulae associated with whatever time integrator it is using, but these values need not be used. To ensure accurate, stable time integration, you can control the size of the time increment used by Abaqus/Standard.

Alternatively, for a general user element in Abaqus/Standard, user subroutine UELMAT may be coded to define the contribution of the element to the model. User subroutine UELMAT is an enhanced version of user subroutine UEL; consequently, all the information provided for user subroutine UEL is also valid for user subroutine UELMAT. The enhancement allows you to access some of the material models from the Abaqus material library from UELMAT. UELMAT works only with a subset of procedures for which UEL is available:

• static;

• direct-integration dynamic;

• frequency extraction;

• steady-state uncouple heat transfer; and

• transient uncouple heat transfer.

Abaqus allows you to access some of the material models from the Abaqus material library from user subroutine UELMAT. The material models are accessed through the utility routines MATERIAL_LIB_MECH and MATERIAL_LIB_HT (“Accessing Abaqus thermal materials,” Section 2.1.18 of the Abaqus User Subroutines Reference Guide, and “Accessing Abaqus materials,” Section 2.1.17 of the Abaqus User Subroutines Reference Guide). Each time user subroutine UELMAT is called with the flags set to values that require computation of the right-hand-side vector and the element Jacobian, the material library must be called for each integration point, where the number of integration points is specified in the element definition (“Specifying the number of integration points” in “User-defined elements,” Section 32.17.1). The material models that are accessible from user subroutine UELMAT are:

• linear elastic model;

• hyperelastic model;

• Ramberg-Osgood model;

• classical metal plasticity models (Mises and Hill);

• extended Drucker-Prager model;

• modified Drucker-Prager/Cap plasticity model;

• porous metal plasticity model;

• elastomeric foam material model; and

• crushable foam plasticity model.

For a general user element in Abaqus/Explicit, user subroutine VUEL must be coded to define the contribution of the element to the model. Abaqus/Explicit calls this routine each time any information about a user-defined element is needed. At each such call Abaqus/Explicit provides the values of the nodal coordinates and of all solution-dependent nodal variables (displacements, velocities, accelerations, etc.) at all degrees of freedom associated with the element, as well as values of the solution-dependent state variables associated with the element at the beginning of the current increment. The incremental displacements are those obtained in a previous increment. Abaqus/Explicit also provides the values of all user-defined properties associated with this element and a control flag array indicating what functions the user subroutine must perform. Depending on this set of control flags, the subroutine must define the contribution of the element to the internal or external force/flux vector, form the mass/capacity matrix, update the solution-dependent state variables associated with the element, and so on.

The element's principal contribution to the model is that it provides nodal forces that depend on the values of the nodal variables , the rate of nodal variables , and on the solution-dependent state variables within the element:

For coupled temperature/displacement elements the temperatures are computed at the beginning of the increment using

More details can be found in “Explicit dynamic analysis,” Section 6.3.3 and “Fully coupled thermal-stress analysis,” Section 6.5.3. The signs of the forces defined in are such that external forces provide positive nodal force values and “internal” forces caused by stresses, damping effects, internal heat fluxes, etc. in the element provide negative nodal force values. Internal forces due to bulk viscosity are dependent on the scaled mass of the element. The necessary information (bulk viscosity constants and mass scaling factors) is passed into the user subroutine for this purpose.

You can apply point loads, moments, fluxes, etc. to the nodes of general user-defined elements in the usual way, using concentrated loads and concentrated fluxes (“Concentrated loads,” Section 34.4.2, and “Thermal loads,” Section 34.4.4).

You can also define distributed loads and fluxes for general user-defined elements (“Distributed loads,” Section 34.4.3, and “Thermal loads,” Section 34.4.4). These loads require a load type key. For user-defined elements, you can define load type keys of the forms Un and, in Abaqus/Standard, UnNU, where n is any positive integer.

If the load type key is of the form Un, the load magnitude is defined directly and follows the standard Abaqus conventions with respect to its amplitude variation as a function of time. In Abaqus/Standard, if the load key is of the form UnNU, all of the load definition will be accomplished inside subroutine UEL and UELMAT. Each time Abaqus/Standard calls subroutine UEL or UELMAT, it tells the subroutine how many distributed loads/fluxes are currently active. For each active load or flux of type Un Abaqus/Standard gives the current magnitude and current increment in magnitude of the load. The coding in subroutine UEL or UELMAT must distribute the loads into consistent equivalent nodal forces and, if necessary, provide their contribution to the Jacobian matrix—the “load stiffness matrix.”

In Abaqus/Explicit only load keys of the form Un can be used, and they can be used only for distributed loads (however, thermal fluxes can be defined in the coding in subroutine VUEL). Each time Abaqus/Explicit calls subroutine VUEL, it tells the subroutine which load number is currently active and the current magnitude of the load. The coding in subroutine VUEL must distribute the loads into consistent equivalent nodal forces.

All quantities to be output must be saved as solution-dependent state variables. In Abaqus/Standard, the solution-dependent state variables can be printed or written to the results file using output variable identifier SDV (“Abaqus/Standard output variable identifiers,” Section 4.2.1).

The components of solution-dependent state variables that belong to a user element are not available in Abaqus/CAE. You can write output to separate files in a table format that can be accessed in Abaqus/CAE to produce history output.

A utility routine GETWAVE is provided in user subroutine UEL to access the wave kinematic data defined for an Abaqus/Aqua analysis (“Abaqus/Aqua analysis,” Section 6.11.1). This utility is discussed in “Obtaining wave kinematic data in an Abaqus/Aqua analysis,” Section 2.1.13 of the Abaqus User Subroutines Reference Guide, where the arguments to GETWAVE and the syntax for its use are defined.

Only node-based surfaces (“Node-based surface definition,” Section 2.3.3) can be created on user-defined elements. Hence, these elements can be used to define only slave surfaces in a contact analysis. In Abaqus/Explicit the user elements will not be included in the general contact algorithm automatically. Node-based surfaces can be defined using these nodes and then included in the general contact definition.

User elements cannot be imported from an Abaqus/Standard analysis into an Abaqus/Explicit analysis or vice versa. Equivalent user elements can be defined in both products to overcome this limitation. However, the state variables associated with these elements will not be communicated.