Products: Abaqus/Standard Abaqus/CAE
The cohesive element fluid flow model:
is typically used in geotechnical applications, where fluid flow continuity within the cohesive element and through the interface must be maintained;
supports the transition from Darcy flow to Poiseuille flow (gap flow) as damage in the element initiates and evolves;
enables modeling of an additional resistance layer on the surface of the cohesive element to model fluid leakoff into the formation;
enables fluid pressure on the cohesive element surface to contribute to its mechanical behavior, which enables the modeling of hydraulically driven fracture;
can be used only in conjunction with traction-separation behavior;
supports fluid flow continuity between intersecting layers of cohesive pore pressure elements; and
enables gravity-induced fluid flux modeling.
The fluid constitutive response consists of the following:
Tangential flow along the cohesive element midplane, which can be modeled as either Darcy or Poiseuille flow; and
Normal flow (also referred to as leakoff) across the cohesive element, which can reflect resistance due to caking or fouling effects.
The flow patterns of the pore fluid in the element are shown in Figure 32.5.7–1. The fluid is assumed to be incompressible, and the formulation is based on a statement of flow continuity that considers tangential and normal flow and the rate of opening of the cohesive element.
Tangential flow in a cohesive element will transition from Darcy flow to Poiseuille flow as damage in the element initiates and evolves. The transition is designed to approximate the changing nature of fluid flow through an initially undamaged porous material (Darcy flow) to flow in a crack (Poiseuille flow) as the material is damaged. You must specify the fluid constitutive response for both types of flow.
The tangential flow equations for the cohesive element are solved within a gap along the length of the element. The gap opening, 
, is defined as
and 
are the current and original cohesive element geometrical thicknesses, respectively; 
is the initial gap opening, which has a default value of 0.002; and 
represents the physical crack opening that is used for Poiseuille flow once the element is damaged. A schematic illustration is shown in Figure 32.5.8–2. is not a physical quantity. It is used by Abaqus/Standard to ensure that the flow equations can be solved robustly when the physical gap is closed (i.e., 
). As increases, the effect of on the flow equations is diminished, as described in “Transition from Darcy flow to Poiseuille flow.”| Input File Usage: | Use the following option to define the initial gap opening directly: |
*SECTION CONTROLS, INITIAL GAP OPENING |
| Abaqus/CAE Usage: | Initial gap opening is not supported in Abaqus/CAE. |
Darcy flow defines a simple relationship between the volumetric flow rate of a fluid and the fluid pressure gradient in a porous material. The relationship is defined by the expression
is the permeability, 
is the pressure gradient along the cohesive element, is the gap opening, and 
is the fluid specific weight.| Input File Usage: | Use the following option to define fully saturated isotropic permeability: |
*PERMEABILITY, TYPE=ISOTROPIC, SPECIFIC= |
| Abaqus/CAE Usage: | Property module: material editor: Other |
In Abaqus/Standard Poiseuille flow within cohesive elements refers to the steady viscous flow between two parallel plates. For this flow, you can specify either a Newtonian fluid or a power law fluid.
In the case of a Newtonian fluid the volume flow rate density vector is given by the expression
is the tangential permeability (the resistance to the fluid flow), is the pressure gradient along the cohesive element, and is the gap opening. Abaqus defines the tangential permeability, or the resistance to flow, according to Reynold's equation:
is the fluid viscosity and is the gap opening. You can also specify an upper limit on the value of .| Input File Usage: | Use the following option to define the tangential flow in a Newtonian fluid: |
*GAP FLOW, TYPE=NEWTONIAN, KMAX |
| Abaqus/CAE Usage: | Property module: material editor: Other |
In the case of a power law fluid the constitutive relation is defined as
is the shear stress, 
is the shear strain rate, 
is the fluid consistency, and 
is the power law coefficient. Abaqus defines the tangential volume flow rate density as 
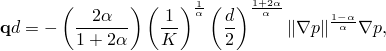
is the gap opening.| Input File Usage: | *GAP FLOW, TYPE=POWER LAW |
| Abaqus/CAE Usage: | Property module: material editor: Other |
You can permit normal flow by defining fluid leak-off coefficients for the pore fluid material. These coefficients define a pressure-flow relationship between the cohesive element's middle nodes and its adjacent surface nodes. The fluid leak-off coefficients can be interpreted as the permeability of a finite layer of material on the cohesive element surfaces, as shown in Figure 32.5.8–3.
The normal flow is defined as
and 
are the flow rates into the top and bottom surfaces, respectively; 
and 
are the fluid leak-off coefficients at the top and bottom element surfaces, respectively; 
is the midface pressure; and 
and 
are the pore pressures on the top and bottom surfaces, respectively.| Input File Usage: | *FLUID LEAKOFF |
| Abaqus/CAE Usage: | Property module: material editor: Other |
You can optionally define leak-off coefficients as functions of temperature and field variables.
| Input File Usage: | *FLUID LEAKOFF, DEPENDENCIES |
| Abaqus/CAE Usage: | Property module: material editor: Other |
User subroutine UFLUIDLEAKOFF can also be used to define more complex leak-off behavior, including the ability to define a time accumulated resistance, or fouling, through the use of solution-dependent state variables.
| Input File Usage: | *FLUID LEAKOFF, USER |
| Abaqus/CAE Usage: | Property module: material editor: Other |
In the presence of a distributed gravity load the tangential flow rate density vector is given by the expression
is the tangential permeability as defined above, 
is the projection of the gravity vector onto the midsurface of the cohesive element, and 
is the pore fluid density. For Darcy flow, 
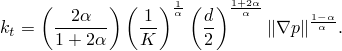
| Input File Usage: | Use the following option to specify the density of the pore fluid: |
*DENSITY, PORE FLUID |
| Abaqus/CAE Usage: | Property module: material editor: General |
For a Newtonian fluid the transition from Darcy flow to Poiseuille flow as a function of the damage variable, 
, is described by the expression
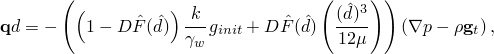
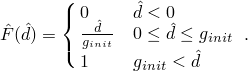
, in a damaged element closes. The flow transition equation for a power law fluid is obtained similarly. You can define an initial gap to identify elements that are fully damaged; that is, 
at the integration points of the elements.
| Input File Usage: | Use the following option to define the initial gap directly: |
*INITIAL CONDITIONS, TYPE=INITIAL GAP element number or element set, omit values for D |
| Abaqus/CAE Usage: | Initial gap definition is not supported in Abaqus/CAE. |
You can define an initial gap to identify elements and assign directly to the integration points. If you assign an initial damage variable to any of the integration points but not all of them, a value of 
is assigned to the integration points to which you did not assign a value.
If an element set is used, you must ensure that all elements within the set have the proper uniform order of integration points.
| Input File Usage: | Use the following option to assign initial damage values: |
*INITIAL CONDITIONS, TYPE=INITIAL GAP element number or element set, D at each integration point |
| Abaqus/CAE Usage: | Initial gap definition is not supported in Abaqus/CAE. |
Your use of cohesive element fluid properties and your property values can impact your solution in some cases.
The pore pressure cohesive element matrices are unsymmetric; therefore, unsymmetric matrix storage and solution may be needed to improve convergence (see “Matrix storage and solution scheme in Abaqus/Standard” in “Defining an analysis,” Section 6.1.2).
You must make sure that the tangential permeability or fluid leak-off coefficients are not excessively large. If either coefficient is many orders of magnitude higher than the permeability in the adjacent continuum elements, matrix conditioning problems may occur, leading to solver singularities and unreliable results.
When different layers of cohesive pore pressure elements intersect, a common midsurface node must be shared by all elements to support fluid flow continuity. Figure 32.5.8–4 shows a two-dimensional mesh example of intersecting elements. Elements 10, 20, 30, and 40 share the same middle node, 100, at the intersecting point.
The following output variables are available when flow is enabled in pore pressure cohesive elements:
GFVR | Gap fluid volume rate. |
PFOPEN | Fracture opening. |
LEAKVRT | Leak-off flow rate at element top. |
ALEAKVRT | Accumulated leak-off flow volume at element top. |
LEAKVRB | Leak-off flow rate at element bottom. |
ALEAKVRB | Accumulated leak-off flow volume at element bottom. |
