
Products: Abaqus/Standard Abaqus/CAE
“Convergence and time integration criteria: overview,” Section 7.2.1
“Implicit dynamic analysis using direct integration,” Section 6.3.2
“Coupled pore fluid diffusion and stress analysis,” Section 6.8.1
“Rate-dependent plasticity: creep and swelling,” Section 23.2.4
“Customizing general solution controls,” Section 14.15.1 of the Abaqus/CAE User's Guide

Abaqus/Standard usually uses automatic time stepping schemes for the solution of transient problems. Factors influencing the increment size for transient problems include convergence aspects related to the degree of geometric, material, and contact nonlinearity (which also influence non-transient problems and are discussed in “Convergence criteria for nonlinear problems,” Section 7.2.3) and the ability of the time integration operator to accurately resolve variations in the accelerations, velocities, and displacements over an increment. This section discusses tolerance parameters and adjustments to the time increment size related to the latter aspect.

Table 7.2.4–1 lists tolerance parameters available for specific analysis procedures. Descriptions of time integrators for the transient procedure types and, in the case of implicit dynamics, discussion of additional factors influencing the time increment size related to accuracy of time integration are provided in the respective sections referenced in Table 7.2.4–1.
Table 7.2.4–1 Time integration accuracy measures for various procedures.
| Procedure | Accuracy measure | Tolerance |
| Implicit dynamics (“Implicit dynamic analysis using direct integration,” Section 6.3.2) | Half-increment residual | Half-increment residual tolerance |
| Transient heat transfer analysis (“Uncoupled heat transfer analysis,” Section 6.5.2) | Temperature increment, | |
| Consolidation analysis (“Coupled pore fluid diffusion and stress analysis,” Section 6.8.1) | Pore pressure increment, | |
| Creep and viscoelastic material behavior (“Rate-dependent plasticity: creep and swelling,” Section 23.2.4) | Creep tolerance |
If ![]() for any control, J, that is active in the step, the time increment
for any control, J, that is active in the step, the time increment ![]() is too large to satisfy that time integration accuracy requirement. The increment is, therefore, begun again with a time increment of
is too large to satisfy that time integration accuracy requirement. The increment is, therefore, begun again with a time increment of
![]()
| Input File Usage: | *CONTROLS, PARAMETERS=TIME INCREMENTATION first data line , , , |
| Abaqus/CAE Usage: | Step module: Other |
If at the current time increment, ![]() ,
,
![]()
![]()
![]()
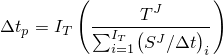
A limit, ![]() , is placed on the time increment increase factor. The default value of
, is placed on the time increment increase factor. The default value of ![]() depends on the type of analysis:
depends on the type of analysis:
![]() = 1.25 for dynamic analysis
= 1.25 for dynamic analysis
![]() = 2.0 for diffusion-dominated processes: creep, transient heat transfer, coupled temperature-displacement, soils consolidation, and transient mass diffusion
= 2.0 for diffusion-dominated processes: creep, transient heat transfer, coupled temperature-displacement, soils consolidation, and transient mass diffusion
![]() = 1.5 for all other cases
= 1.5 for all other cases
If the problem is nonlinear, the time increment may be restricted by the rate of convergence of the nonlinear equations. The time incrementation controls used with nonlinear problems are described in “Convergence criteria for nonlinear problems,” Section 7.2.3.
| Input File Usage: | *CONTROLS, PARAMETERS=TIME INCREMENTATION , , , , , , , , , |
| Abaqus/CAE Usage: | Step module: Other |

In linear transient problems when Abaqus/Standard uses implicit integration, the system of equations must be reformed and decomposed whenever the time increment changes even though the stiffness matrix does not change. Therefore, to reduce the number of increments at which the system matrix changes, Abaqus/Standard makes use of the factor ![]() , where
, where
![]()
![]()
| Input File Usage: | *CONTROLS, PARAMETERS=TIME INCREMENTATION first data line second data line , , , , |
| Abaqus/CAE Usage: | Step module: Other |