Product: Abaqus/Standard
Warning: The use of this subroutine generally requires considerable expertise. You are cautioned that the implementation of any realistic constitutive model requires extensive development and testing. Initial testing on a single-element model with prescribed traction loading is strongly recommended.

User subroutine UMAT:
can be used to define the mechanical constitutive behavior of a material;
will be called at all material calculation points of elements for which the material definition includes a user-defined material behavior;
can be used with any procedure that includes mechanical behavior;
can use solution-dependent state variables;
must update the stresses and solution-dependent state variables to their values at the end of the increment for which it is called;
must provide the material Jacobian matrix, ![]() , for the mechanical constitutive model;
, for the mechanical constitutive model;
can be used in conjunction with user subroutine USDFLD to redefine any field variables before they are passed in; and
is described further in “User-defined mechanical material behavior,” Section 26.7.1 of the Abaqus Analysis User's Guide.

In the stress and strain arrays and in the matrices DDSDDE, DDSDDT, and DRPLDE, direct components are stored first, followed by shear components. There are NDI direct and NSHR engineering shear components. The order of the components is defined in “Conventions,” Section 1.2.2 of the Abaqus Analysis User's Guide. Since the number of active stress and strain components varies between element types, the routine must be coded to provide for all element types with which it will be used.

If a local orientation (“Orientations,” Section 2.2.5 of the Abaqus Analysis User's Guide) is used at the same point as user subroutine UMAT, the stress and strain components will be in the local orientation; and, in the case of finite-strain analysis, the basis system in which stress and strain components are stored rotates with the material.

You should ensure that the integration scheme coded in this routine is stable—no direct provision is made to include a stability limit in the time stepping scheme based on the calculations in UMAT.

DDSDDE and—for coupled temperature-displacement and coupled thermal-electrical-structural analyses—DDSDDT, DRPLDE, and DRPLDT must be defined accurately if rapid convergence of the overall Newton scheme is to be achieved. In most cases the accuracy of this definition is the most important factor governing the convergence rate. Since nonsymmetric equation solution is as much as four times as expensive as the corresponding symmetric system, if the constitutive Jacobian (DDSDDE) is only slightly nonsymmetric (for example, a frictional material with a small friction angle), it may be less expensive computationally to use a symmetric approximation and accept a slower convergence rate.
An incorrect definition of the material Jacobian affects only the convergence rate; the results (if obtained) are unaffected.

The constitutive Jacobian (DDSDDE) must provide both the stiffness (storage modulus) and damping (loss modulus) for modeling frequency domain viscoelastic behavior.

There are several special considerations that need to be noted.
The deformation gradient is available for solid (continuum) elements, membranes, and finite-strain shells (S3/S3R, S4, S4R, SAXs, and SAXAs). It is not available for beams or small-strain shells. It is stored as a 3 × 3 matrix with component equivalence DFGRD0(I,J) ![]() . For fully integrated first-order isoparametric elements (4-node quadrilaterals in two dimensions and 8-node hexahedra in three dimensions) the selectively reduced integration technique is used (also known as the
. For fully integrated first-order isoparametric elements (4-node quadrilaterals in two dimensions and 8-node hexahedra in three dimensions) the selectively reduced integration technique is used (also known as the ![]() technique). Thus, a modified deformation gradient
technique). Thus, a modified deformation gradient
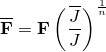
The deformation gradient, which is passed to the user subroutine, is computed with respect to the initial configuration. If a local orientation is not specified, the components of the deformation gradient are expressed in the global coordinate system. If a local orientation is used, the components of the same deformation gradient are expressed in the local coordinate system; in the case of finite-strain analysis, the basis system rotates with the material.
If user subroutine UMAT is used to describe the material of beams or shells that calculate transverse shear energy, you must specify the transverse shear stiffness as part of the beam or shell section definition to define the transverse shear behavior. See “Shell section behavior,” Section 29.6.4 of the Abaqus Analysis User's Guide, and “Choosing a beam element,” Section 29.3.3 of the Abaqus Analysis User's Guide, for information on specifying this stiffness.
When user subroutine UMAT is used to describe the material response of beams with open sections (for example, an I-section), the torsional stiffness is obtained as
![]()
If this capability is used to describe the material of elements with hourglassing modes, you must define the hourglass stiffness factor for hourglass control based on the total stiffness approach as part of the element section definition. The hourglass stiffness factor is not required for enhanced hourglass control, but you can define a scaling factor for the stiffness associated with the drill degree of freedom (rotation about the surface normal). See “Section controls,” Section 27.1.4 of the Abaqus Analysis User's Guide, for information on specifying the stiffness factor.
The constitutive behavior of the pipe-soil interaction elements (see “Pipe-soil interaction elements,” Section 32.12.1 of the Abaqus Analysis User's Guide) is defined by the force per unit length caused by relative displacement between two edges of the element. The relative-displacements are available as “strains” (STRAN and DSTRAN). The corresponding forces per unit length must be defined in the STRESS array. The Jacobian matrix defines the variation of force per unit length with respect to relative displacement.
For two-dimensional elements two in-plane components of “stress” and “strain” exist (NTENS=NDI=2, and NSHR=0). For three-dimensional elements three components of “stress” and “strain” exist (NTENS=NDI=3, and NSHR=0).

If the material model allows large volume changes and geometric nonlinearity is considered, the exact definition of the consistent Jacobian should be used to ensure rapid convergence. These conditions are most commonly encountered when considering either large elastic strains or pressure-dependent plasticity. In the former case, total-form constitutive equations relating the Cauchy stress to the deformation gradient are commonly used; in the latter case, rate-form constitutive laws are generally used.
For total-form constitutive laws, the exact consistent Jacobian ![]() is defined through the variation in Kirchhoff stress:
is defined through the variation in Kirchhoff stress:
![]()
![]()
![]()
For rate-form constitutive laws, the exact consistent Jacobian is given by
![]()

For user-defined almost incompressible or incompressible elastic materials, a few different options are available depending on whether hybrid or nonhybrid elements are used. For all cases the first option should be to use user subroutine UHYPER instead of user subroutine UMAT when it is possible to do so. In user subroutine UMAT incompressible materials can be modeled via a penalty method; that is, you ensure that a finite bulk modulus is used. The bulk modulus should be large enough to model incompressibility sufficiently but small enough to avoid loss of precision. As a general guideline, the bulk modulus should be about ![]() –
–![]() times the shear modulus. The tangent bulk modulus
times the shear modulus. The tangent bulk modulus ![]() can be calculated from
can be calculated from
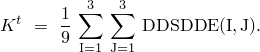
If a hybrid element is used with user subroutine UMAT, Abaqus/Standard, by default, replaces the pressure stress calculated from your definition of STRESS with that derived from the Lagrange multiplier and modifies the Jacobian appropriately (“Hybrid incompressible solid element formulation,” Section 3.2.3 of the Abaqus Theory Guide). This approach is suitable for material models that use an incremental formulation (for example, metal plasticity) but is not consistent with a total formulation that is commonly used for hyperelastic materials. In the latter situation, the default formulation may lead to convergence problems. Such convergence problems may be observed, for example, when an almost incompressible nonlinear elastic user material is subjected to large deformations. Abaqus/Standard provides an alternate total formulation when user materials are used with hybrid elements (see “User-defined mechanical material behavior,” Section 26.7.1 of the Abaqus Analysis User's Guide). This formulation is consistent with the native almost incompressible formulation used by Abaqus for hyperelastic materials (“Hyperelastic material behavior,” Section 4.6.1 of the Abaqus Theory Guide) and works better than the default formulation for such cases.
The total hybrid formulation assumes that the response of the material can be written as the sum of its deviatoric and volumetric parts and that these parts are decoupled from each other. In particular, the volumetric response is assumed to be defined in terms of a strain energy potential, ![]() , which is a function of an alternate variable,
, which is a function of an alternate variable, ![]() in place of the actual volume change
in place of the actual volume change ![]() . The alternate variable is made available inside user subroutine UMAT by extending the STRESS array beyond NTENS, with the NTENS+1 entry providing read access to
. The alternate variable is made available inside user subroutine UMAT by extending the STRESS array beyond NTENS, with the NTENS+1 entry providing read access to ![]() . You must define the hydrostatic part of the stress tensor as
. You must define the hydrostatic part of the stress tensor as ![]() . The formulation also requires the additional derivatives
. The formulation also requires the additional derivatives ![]() and
and ![]() . You must define these additional derivatives inside user subroutine UMAT as the NTENS+1 and the NTENS+2 entry, respectively, of the STRESS array. In addition, the bulk modulus of the material (contributes toward the material Jacobian matrix, DDSDDE) must be defined as
. You must define these additional derivatives inside user subroutine UMAT as the NTENS+1 and the NTENS+2 entry, respectively, of the STRESS array. In addition, the bulk modulus of the material (contributes toward the material Jacobian matrix, DDSDDE) must be defined as ![]()
Abaqus/Standard also provides a fully incompressible user material formulation for use with hybrid elements to define a fully incompressible user material response. This formulation is consistent with the native formulation used by Abaqus for incompressible hyperelastic materials and assumes that the deviatoric stress can be derived from a strain energy potential function. You need define only the deviatoric stress and Jacobian to define a fully incompressible material response through user subroutine UMAT.
For incompressible pressure-sensitive materials the element choice is particularly important when using user subroutine UMAT. In particular, first-order wedge elements should be avoided. For these elements the ![]() technique is not used to alter the deformation gradient that is passed into user subroutine UMAT, which increases the risk of volumetric locking.
technique is not used to alter the deformation gradient that is passed into user subroutine UMAT, which increases the risk of volumetric locking.

Abaqus/Standard passes zero strain increments into user subroutine UMAT to start the first increment of all the steps and all increments of steps for which you have suppressed extrapolation (see “Defining an analysis,” Section 6.1.2 of the Abaqus Analysis User's Guide). In this case you can define only the Jacobian (DDSDDE).

Several utility routines may help in coding user subroutine UMAT. Their functions include determining stress invariants for a stress tensor and calculating principal values and directions for stress or strain tensors. These utility routines are discussed in detail in “Obtaining stress invariants, principal stress/strain values and directions, and rotating tensors in an Abaqus/Standard analysis,” Section 2.1.11.

SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
1 RPL,DDSDDT,DRPLDE,DRPLDT,
2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
C
INCLUDE 'ABA_PARAM.INC'
C
CHARACTER*80 CMNAME
DIMENSION STRESS(NTENS),STATEV(NSTATV),
1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
4 JSTEP(4)
user coding to define DDSDDE, STRESS, STATEV, SSE, SPD, SCD
and, if necessary, RPL, DDSDDT, DRPLDE, DRPLDT, PNEWDT
RETURN
END
DDSDDE(NTENS,NTENS)
Jacobian matrix of the constitutive model, ![]() , where
, where ![]() are the stress increments and
are the stress increments and ![]() are the strain increments. DDSDDE(I,J) defines the change in the Ith stress component at the end of the time increment caused by an infinitesimal perturbation of the Jth component of the strain increment array. Unless you invoke the unsymmetric equation solution capability for the user-defined material, Abaqus/Standard will use only the symmetric part of DDSDDE. The symmetric part of the matrix is calculated by taking one half the sum of the matrix and its transpose.
are the strain increments. DDSDDE(I,J) defines the change in the Ith stress component at the end of the time increment caused by an infinitesimal perturbation of the Jth component of the strain increment array. Unless you invoke the unsymmetric equation solution capability for the user-defined material, Abaqus/Standard will use only the symmetric part of DDSDDE. The symmetric part of the matrix is calculated by taking one half the sum of the matrix and its transpose.
For viscoelastic behavior in the frequency domain, the Jacobian matrix must be dimensioned as DDSDDE(NTENS,NTENS,2). The stiffness contribution (storage modulus) must be provided in DDSDDE(NTENS,NTENS,1), while the damping contribution (loss modulus) must be provided in DDSDDE(NTENS,NTENS,2).
STRESS(NTENS)
This array is passed in as the stress tensor at the beginning of the increment and must be updated in this routine to be the stress tensor at the end of the increment. If you specified initial stresses (“Initial conditions in Abaqus/Standard and Abaqus/Explicit,” Section 34.2.1 of the Abaqus Analysis User's Guide), this array will contain the initial stresses at the start of the analysis. The size of this array depends on the value of NTENS as defined below. In finite-strain problems the stress tensor has already been rotated to account for rigid body motion in the increment before UMAT is called, so that only the corotational part of the stress integration should be done in UMAT. The measure of stress used is “true” (Cauchy) stress.
If the UMAT utilizes a hybrid formulation that is total (as opposed to the default incremental behavior), the stress array is extended beyond NTENS. The first NTENS entries of the array contain the stresses, as described above. The additional quantities are as follows:
STRESS(NTENS+1)
Read only: ![]() ,
,
STRESS(NTENS+2)
Write only: ![]() , and
, and
STRESS(NTENS+3)
Write only: ![]() , where
, where ![]() is the volumetric part of the strain energy density potential.
is the volumetric part of the strain energy density potential.
STATEV(NSTATV)
An array containing the solution-dependent state variables. These are passed in as the values at the beginning of the increment unless they are updated in user subroutines USDFLD or UEXPAN, in which case the updated values are passed in. In all cases STATEV must be returned as the values at the end of the increment. The size of the array is defined as described in “Allocating space” in “User subroutines: overview,” Section 18.1.1 of the Abaqus Analysis User's Guide.
In finite-strain problems any vector-valued or tensor-valued state variables must be rotated to account for rigid body motion of the material, in addition to any update in the values associated with constitutive behavior. The rotation increment matrix, DROT, is provided for this purpose.
SSE, SPD, SCD
Specific elastic strain energy, plastic dissipation, and “creep” dissipation, respectively. These are passed in as the values at the start of the increment and should be updated to the corresponding specific energy values at the end of the increment. They have no effect on the solution, except that they are used for energy output.
RPL
Volumetric heat generation per unit time at the end of the increment caused by mechanical working of the material.
DDSDDT(NTENS)
Variation of the stress increments with respect to the temperature.
DRPLDE(NTENS)
Variation of RPL with respect to the strain increments.
DRPLDT
Variation of RPL with respect to the temperature.
RPL
RPL is used to indicate whether or not a cohesive element is open to the tangential flow of pore fluid. Set RPL equal to 0 if there is no tangential flow; otherwise, assign a nonzero value to RPL if an element is open. Once opened, a cohesive element will remain open to the fluid flow.

PNEWDT
Ratio of suggested new time increment to the time increment being used (DTIME, see discussion later in this section). This variable allows you to provide input to the automatic time incrementation algorithms in Abaqus/Standard (if automatic time incrementation is chosen). For a quasi-static procedure the automatic time stepping that Abaqus/Standard uses, which is based on techniques for integrating standard creep laws (see “Quasi-static analysis,” Section 6.2.5 of the Abaqus Analysis User's Guide), cannot be controlled from within the UMAT subroutine.
PNEWDT is set to a large value before each call to UMAT.
If PNEWDT is redefined to be less than 1.0, Abaqus/Standard must abandon the time increment and attempt it again with a smaller time increment. The suggested new time increment provided to the automatic time integration algorithms is PNEWDT × DTIME, where the PNEWDT used is the minimum value for all calls to user subroutines that allow redefinition of PNEWDT for this iteration.
If PNEWDT is given a value that is greater than 1.0 for all calls to user subroutines for this iteration and the increment converges in this iteration, Abaqus/Standard may increase the time increment. The suggested new time increment provided to the automatic time integration algorithms is PNEWDT × DTIME, where the PNEWDT used is the minimum value for all calls to user subroutines for this iteration.
If automatic time incrementation is not selected in the analysis procedure, values of PNEWDT that are greater than 1.0 will be ignored and values of PNEWDT that are less than 1.0 will cause the job to terminate.

STRAN(NTENS)
An array containing the total strains at the beginning of the increment. If thermal expansion is included in the same material definition, the strains passed into UMAT are the mechanical strains only (that is, the thermal strains computed based upon the thermal expansion coefficient have been subtracted from the total strains). These strains are available for output as the “elastic” strains.
In finite-strain problems the strain components have been rotated to account for rigid body motion in the increment before UMAT is called and are approximations to logarithmic strain.
DSTRAN(NTENS)
Array of strain increments. If thermal expansion is included in the same material definition, these are the mechanical strain increments (the total strain increments minus the thermal strain increments).
TIME(1)
Value of step time at the beginning of the current increment or frequency.
TIME(2)
Value of total time at the beginning of the current increment.
DTIME
Time increment.
TEMP
Temperature at the start of the increment.
DTEMP
Increment of temperature.
PREDEF
Array of interpolated values of predefined field variables at this point at the start of the increment, based on the values read in at the nodes.
DPRED
Array of increments of predefined field variables.
CMNAME
User-defined material name, left justified. Some internal material models are given names starting with the “ABQ_” character string. To avoid conflict, you should not use “ABQ_” as the leading string for CMNAME.
NDI
Number of direct stress components at this point.
NSHR
Number of engineering shear stress components at this point.
NTENS
Size of the stress or strain component array (NDI + NSHR).
NSTATV
Number of solution-dependent state variables that are associated with this material type (defined as described in “Allocating space” in “User subroutines: overview,” Section 18.1.1 of the Abaqus Analysis User's Guide).
PROPS(NPROPS)
User-specified array of material constants associated with this user material.
NPROPS
User-defined number of material constants associated with this user material.
COORDS
An array containing the coordinates of this point. These are the current coordinates if geometric nonlinearity is accounted for during the step (see “Defining an analysis,” Section 6.1.2 of the Abaqus Analysis User's Guide); otherwise, the array contains the original coordinates of the point.
DROT(3,3)
Rotation increment matrix. This matrix represents the increment of rigid body rotation of the basis system in which the components of stress (STRESS) and strain (STRAN) are stored. It is provided so that vector- or tensor-valued state variables can be rotated appropriately in this subroutine: stress and strain components are already rotated by this amount before UMAT is called. This matrix is passed in as a unit matrix for small-displacement analysis and for large-displacement analysis if the basis system for the material point rotates with the material (as in a shell element or when a local orientation is used).
CELENT
Characteristic element length, which is a typical length of a line across an element for a first-order element; it is half of the same typical length for a second-order element. For beams and trusses it is a characteristic length along the element axis. For membranes and shells it is a characteristic length in the reference surface. For axisymmetric elements it is a characteristic length in the ![]() plane only. For cohesive elements it is equal to the constitutive thickness.
plane only. For cohesive elements it is equal to the constitutive thickness.
DFGRD0(3,3)
Array containing the deformation gradient at the beginning of the increment. If a local orientation is defined at the material point, the deformation gradient components are expressed in the local coordinate system defined by the orientation at the beginning of the increment. For a discussion regarding the availability of the deformation gradient for various element types, see “Deformation gradient.”
DFGRD1(3,3)
Array containing the deformation gradient at the end of the increment. If a local orientation is defined at the material point, the deformation gradient components are expressed in the local coordinate system defined by the orientation. This array is set to the identity matrix if nonlinear geometric effects are not included in the step definition associated with this increment. For a discussion regarding the availability of the deformation gradient for various element types, see “Deformation gradient.”
NOEL
Element number.
NPT
Integration point number.
LAYER
Layer number (for composite shells and layered solids).
KSPT
Section point number within the current layer.
JSTEP(1)
Step number.
JSTEP(2)
Procedure type key (see “Results file output format,” Section 5.1.2 of the Abaqus Analysis User's Guide).
JSTEP(3)
1 if NLGEOM=YES for the current step; 0 otherwise.
JSTEP(4)
1 if current step is a linear perturbation procedure; 0 otherwise.
KINC
Increment number.

To use more than one user-defined mechanical material model, the variable CMNAME can be tested for different material names inside user subroutine UMAT as illustrated below:
IF (CMNAME(1:4) .EQ. 'MAT1') THEN CALL UMAT_MAT1(argument_list) ELSE IF(CMNAME(1:4) .EQ. 'MAT2') THEN CALL UMAT_MAT2(argument_list) END IFUMAT_MAT1 and UMAT_MAT2 are the actual user material subroutines containing the constitutive material models for each material MAT1 and MAT2, respectively. Subroutine UMAT merely acts as a directory here. The argument list may be the same as that used in subroutine UMAT.

As a simple example of the coding of user subroutine UMAT, consider the linear, viscoelastic model shown in Figure 1.1.44–1. Although this is not a very useful model for real materials, it serves to illustrate how to code the routine.
The behavior of the one-dimensional model shown in the figure is
![]()
![]()
![]()
![]()
A simple, stable integration operator for this equation is the central difference operator:
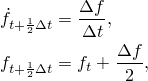
Applying this to the rate constitutive equations above gives
![]()
![]()
![]()
![]()
![]()
The total change in specific energy in an increment for this material is
![]()
![]()
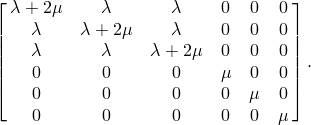
No state variables are needed for this material, so the allocation of space for them is not necessary. In a more realistic case a set of parallel models of this type might be used, and the stress components in each model might be stored as state variables.
For our simple case a user material definition can be used to read in the five constants in the order ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() so that
so that
![]()
![]()
![]()
![]()
![]()
SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
1 RPL,DDSDDT,DRPLDE,DRPLDT,
2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
C
INCLUDE 'ABA_PARAM.INC'
C
CHARACTER*80 CMNAME
DIMENSION STRESS(NTENS),STATEV(NSTATV),
1 DDSDDE(NTENS,NTENS),
2 DDSDDT(NTENS),DRPLDE(NTENS),
3 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
4 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
5 JSTEP(4)
DIMENSION DSTRES(6),D(3,3)
C
C EVALUATE NEW STRESS TENSOR
C
EV = 0.
DEV = 0.
DO K1=1,NDI
EV = EV + STRAN(K1)
DEV = DEV + DSTRAN(K1)
END DO
C
TERM1 = .5*DTIME + PROPS(5)
TERM1I = 1./TERM1
TERM2 = (.5*DTIME*PROPS(1)+PROPS(3))*TERM1I*DEV
TERM3 = (DTIME*PROPS(2)+2.*PROPS(4))*TERM1I
C
DO K1=1,NDI
DSTRES(K1) = TERM2+TERM3*DSTRAN(K1)
1 +DTIME*TERM1I*(PROPS(1)*EV
2 +2.*PROPS(2)*STRAN(K1)-STRESS(K1))
STRESS(K1) = STRESS(K1) + DSTRES(K1)
END DO
C
TERM2 = (.5*DTIME*PROPS(2) + PROPS(4))*TERM1I
I1 = NDI
DO K1=1,NSHR
I1 = I1+1
DSTRES(I1) = TERM2*DSTRAN(I1)+
1 DTIME*TERM1I*(PROPS(2)*STRAN(I1)-STRESS(I1))
STRESS(I1) = STRESS(I1)+DSTRES(I1)
END DO
C
C CREATE NEW JACOBIAN
C
TERM2 = (DTIME*(.5*PROPS(1)+PROPS(2))+PROPS(3)+
1 2.*PROPS(4))*TERM1I
TERM3 = (.5*DTIME*PROPS(1)+PROPS(3))*TERM1I
DO K1=1,NTENS
DO K2=1,NTENS
DDSDDE(K2,K1) = 0.
END DO
END DO
C
DO K1=1,NDI
DDSDDE(K1,K1) = TERM2
END DO
C
DO K1=2,NDI
N2 = K1–1
DO K2=1,N2
DDSDDE(K2,K1) = TERM3
DDSDDE(K1,K2) = TERM3
END DO
END DO
TERM2 = (.5*DTIME*PROPS(2)+PROPS(4))*TERM1I
I1 = NDI
DO K1=1,NSHR
I1 = I1+1
DDSDDE(I1,I1) = TERM2
END DO
C
C TOTAL CHANGE IN SPECIFIC ENERGY
C
TDE = 0.
DO K1=1,NTENS
TDE = TDE + (STRESS(K1)-.5*DSTRES(K1))*DSTRAN(K1)
END DO
C
C CHANGE IN SPECIFIC ELASTIC STRAIN ENERGY
C
TERM1 = PROPS(1) + 2.*PROPS(2)
DO K1=1,NDI
D(K1,K1) = TERM1
END DO
DO K1=2,NDI
N2 = K1-1
DO K2=1,N2
D(K1,K2) = PROPS(1)
D(K2,K1) = PROPS(1)
END DO
END DO
DEE = 0.
DO K1=1,NDI
TERM1 = 0.
TERM2 = 0.
DO K2=1,NDI
TERM1 = TERM1 + D(K1,K2)*STRAN(K2)
TERM2 = TERM2 + D(K1,K2)*DSTRAN(K2)
END DO
DEE = DEE + (TERM1+.5*TERM2)*DSTRAN(K1)
END DO
I1 = NDI
DO K1=1,NSHR
I1 = I1+1
DEE = DEE + PROPS(2)*(STRAN(I1)+.5*DSTRAN(I1))*DSTRAN(I1)
END DO
SSE = SSE + DEE
SCD = SCD + TDE – DEE
RETURN
END