Product: Abaqus/Standard
User subroutine UANISOHYPER_INV:
can be used to define the strain energy potential of anisotropic hyperelastic materials as a function of an irreducible set of scalar invariants;
is called at all material calculation points of elements for which the material definition contains user-defined anisotropic hyperelastic behavior with an invariant-based formulation (“Anisotropic hyperelastic behavior,” Section 22.5.3 of the Abaqus Analysis User's Guide);
can include material behavior dependent on field variables or state variables;
requires that the values of the derivatives of the strain energy density function of the anisotropic hyperelastic material be defined with respect to the scalar invariants; and
is called twice per material point in each iteration.
To facilitate coding and provide easy access to the array of invariants passed to user subroutine UANISOHYPER_INV, an enumerated representation of each invariant is introduced. Any scalar invariant can, therefore, be represented uniquely by an enumerated invariant, 
, where the subscript n denotes the order of the invariant according to the enumeration scheme in the following table:
For example, in the case of three families of fibers there are a total of 15 invariants: 
, 
, 
, six invariants of type 
, and six invariants of type 
, with 
. The following correspondence exists between each of these invariants and their enumerated counterpart:
A similar scheme is used for the array ZETA of terms 
. Each term can be represented uniquely by an enumerated counterpart 
, as shown below:
terms: 
, 
, and 
. These are stored in the ZETA array as 
.The components of the array UI1 of first derivatives of the strain energy potential with respect to the scalar invariants, 
, are stored using the enumeration scheme discussed above for the scalar invariants.
The elements of the array UI2 of second derivatives of the strain energy function, 
, are laid out in memory using triangular storage: if 
denotes the component in this array corresponding to the term , then 
. For example, the term 
is stored in component 
in the UI2 array.
There are several special considerations that need to be noted.
When UANISOHYPER_INV is used to define the material response of shell elements that calculate transverse shear energy, Abaqus/Standard cannot calculate a default value for the transverse shear stiffness of the element. Hence, you must define the element's transverse shear stiffness. See “Shell section behavior,” Section 29.6.4 of the Abaqus Analysis User's Guide, for guidelines on choosing this stiffness.
When UANISOHYPER_INV is used to define the material response of elements with hourglassing modes, you must define the hourglass stiffness for hourglass control based on the total stiffness approach. The hourglass stiffness is not required for enhanced hourglass control, but you can define a scaling factor for the stiffness associated with the drill degree of freedom (rotation about the surface normal). See “Section controls,” Section 27.1.4 of the Abaqus Analysis User's Guide.
SUBROUTINE UANISOHYPER_INV (AINV, UA, ZETA, NFIBERS, NINV,
1 UI1, UI2, UI3, TEMP, NOEL, CMNAME, INCMPFLAG, IHYBFLAG,
2 NUMSTATEV, STATEV, NUMFIELDV, FIELDV, FIELDVINC,
3 NUMPROPS, PROPS)
C
INCLUDE 'ABA_PARAM.INC'
C
CHARACTER*80 CMNAME
DIMENSION AINV(NINV), UA(2),
2 ZETA(NFIBERS*(NFIBERS-1)/2)), UI1(NINV),
3 UI2(NINV*(NINV+1)/2), UI3(NINV*(NINV+1)/2),
4 STATEV(NUMSTATEV), FIELDV(NUMFIELDV),
5 FIELDVINC(NUMFIELDV), PROPS(NUMPROPS)
user coding to define UA,UI1,UI2,UI3,STATEV
RETURN
END
UA(1)
U, strain energy density function. For a compressible material at least one derivative involving J should be nonzero. For an incompressible material all derivatives involving J are ignored.
UA(2)
, the deviatoric part of the strain energy density of the primary material response. This quantity is needed only if the current material definition also includes Mullins effect (see “Mullins effect,” Section 22.6.1 of the Abaqus Analysis User's Guide).
UI1(NINV)
Array of derivatives of strain energy potential with respect to the scalar invariants, , ordered using the enumeration scheme discussed above.
UI2(NINV*(NINV+1)/2)
Array of second derivatives of strain energy potential with respect to the scalar invariants (using triangular storage), .
UI3(NINV*(NINV+1)/2)
Array of derivatives with respect to J of the second derivatives of the strain energy potential (using triangular storage), 
. This quantity is needed only for compressible materials with a hybrid formulation (when INCMPFLAG = 0 and IHYBFLAG = 1).
STATEV
Array containing the user-defined solution-dependent state variables at this point. These are supplied as values at the start of the increment or as values updated by other user subroutines (see “User subroutines: overview,” Section 18.1.1 of the Abaqus Analysis User's Guide) and must be returned as values at the end of the increment.
NFIBERS
Number of families of fibers defined for this material.
NINV
Number of scalar invariants.
TEMP
Current temperature at this point.
NOEL
Element number.
CMNAME
User-specified material name, left justified.
INCMPFLAG
Incompressibility flag defined to be 1 if the material is specified as incompressible or 0 if the material is specified as compressible.
IHYBFLAG
Hybrid formulation flag defined to be 1 for hybrid elements; 0 otherwise.
NUMSTATEV
User-defined number of solution-dependent state variables associated with this material (see “Allocating space” in “User subroutines: overview,” Section 18.1.1 of the Abaqus Analysis User's Guide).
NUMFIELDV
Number of field variables.
FIELDV
Array of interpolated values of predefined field variables at this material point at the end of the increment based on the values read in at the nodes (initial values at the beginning of the analysis and current values during the analysis).
FIELDVINC
Array of increments of predefined field variables at this material point for this increment, including any values updated by user subroutine USDFLD.
NUMPROPS
Number of material properties entered for this user-defined hyperelastic material.
PROPS
Array of material properties entered for this user-defined hyperelastic material.
AINV(NINV)
Array of scalar invariants, 
, at each material point at the end of the increment. The invariants are ordered using the enumeration scheme discussed above.
ZETA(NFIBERS*(NFIBERS-1)/2))
Array of dot product between the directions of different families of fiber in the reference configuration, . The array contains the enumerated values using the scheme discussed above.
As an example of the coding of user subroutine UANISOHYPER_INV, consider the model proposed by Kaliske and Schmidt (2005) for nonlinear anisotropic elasticity with two families of fibers. The strain energy function is given by a polynomial series expansion in the form
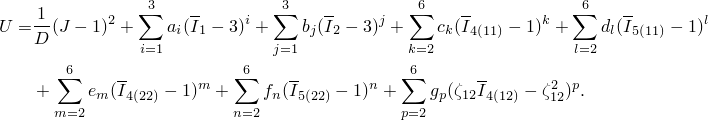
The code in user subroutine UANISOHYPER_INV must return the derivatives of the strain energy function with respect to the scalar invariants, which are readily computed from the above expression. In this example auxiliary functions are used to facilitate enumeration of pseudo-invariants of type 
and 
, as well as for indexing into the array of second derivatives using symmetric storage. The user subroutine would be coded as follows:
subroutine uanisohyper_inv (aInv, ua, zeta, nFibers, nInv,
* ui1, ui2, ui3, temp, noel,
* cmname, incmpFlag, ihybFlag,
* numStatev, statev,
* numFieldv, fieldv, fieldvInc,
* numProps, props)
C
include 'aba_param.inc'
C
character *80 cmname
dimension aInv(nInv), ua(2), zeta(nFibers*(nFibers-1)/2)
dimension ui1(nInv), ui2(nInv*(nInv+1)/2)
dimension ui3(nInv*(nInv+1)/2), statev(numStatev)
dimension fieldv(numFieldv), fieldvInc(numFieldv)
dimension props(numProps)
C
parameter ( zero = 0.d0,
* one = 1.d0,
* two = 2.d0,
* three = 3.d0,
* four = 4.d0,
* five = 5.d0,
* six = 6.d0 )
C
C Kaliske-Schmidtt energy function (3D)
C
C Read material properties
d=props(1)
dInv = one / d
a1=props(2)
a2=props(3)
a3=props(4)
b1=props(5)
b2=props(6)
b3=props(7)
c2=props(8)
c3=props(9)
c4=props(10)
c5=props(11)
c6=props(12)
d2=props(13)
d3=props(14)
d4=props(15)
d5=props(16)
d6=props(17)
e2=props(18)
e3=props(19)
e4=props(20)
e5=props(21)
e6=props(22)
f2=props(23)
f3=props(24)
f4=props(25)
f5=props(26)
f6=props(27)
g2=props(28)
g3=props(29)
g4=props(30)
g5=props(31)
g6=props(32)
C
C Compute Udev and 1st and 2nd derivatives w.r.t invariants
C - I1
bi1 = aInv(1)
term = bi1-three
ua(2) = a1*term + a2*term**2 + a3*term**3
ui1(1) = a1 + two*a2*term + three*a3*term**2
ui2(indx(1,1)) = two*a2 + three*two*a3*term
C - I2
bi2 = aInv(2)
term = bi2-three
ua(2) = ua(2) + b1*term + b2*term**2 + b3*term**3
ui1(2) = b1 + two*b2*term + three*b3*term**2
ui2(indx(2,2)) = two*b2 + three*two*b3*term
C - I3 (=J)
bi3 = aInv(3)
term = bi3-one
ui1(3) = two*dInv*term
ui2(indx(3,3)) = two*dInv
C - I4(11)
nI411 = indxInv4(1,1)
bi411 = aInv(nI411)
term = bi411-one
ua(2) = ua(2)
* + c2*term**2 + c3*term**3 + c4*term**4
* + c5*term**5 + c6*term**6
ui1(nI411) =
* two*c2*term
* + three*c3*term**2
* + four*c4*term**3
* + five*c5*term**4
* + six*c6*term**5
ui2(indx(nI411,nI411)) =
* two*c2
* + three*two*c3*term
* + four*three*c4*term**2
* + five*four*c5*term**3
* + six*five*c6*term**4
C - I5(11)
nI511 = indxInv5(1,1)
bi511 = aInv(nI511)
term = bi511-one
ua(2) = ua(2)
* + d2*term**2 + d3*term**3 + d4*term**4
* + d5*term**5 + d6*term**6
ui1(nI511) =
* two*d2*term
* + three*d3*term**2
* + four*d4*term**3
* + five*d5*term**4
* + six*d6*term**5
ui2(indx(nI511,nI511)) =
* two*d2
* + three*two*d3*term
* + four*three*d4*term**2
* + five*four*d5*term**3
* + six*five*d6*term**4
C - I4(22)
nI422 = indxInv4(2,2)
bi422 = aInv(nI422)
term = bi422-one
ua(2) = ua(2)
* + e2*term**2 + e3*term**3 + e4*term**4
* + e5*term**5 + e6*term**6
ui1(nI422) =
* two*e2*term
* + three*e3*term**2
* + four*e4*term**3
* + five*e5*term**4
* + six*e6*term**5
ui2(indx(nI422,nI422)) =
* two*e2
* + three*two*e3*term
* + four*three*e4*term**2
* + five*four*e5*term**3
* + six*five*e6*term**4
C - I5(22)
nI522 = indxInv5(2,2)
bi522 = aInv(nI522)
term = bi522-one
ua(2) = ua(2)
* + f2*term**2 + f3*term**3 + f4*term**4
* + f5*term**5 + f6*term**6
ui1(nI522) =
* two*f2*term
* + three*f3*term**2
* + four*f4*term**3
* + five*f5*term**4
* + six*f6*term**5
ui2(indx(nI522,nI522)) =
* two*f2
* + three*two*f3*term
* + four*three*f4*term**2
* + five*four*f5*term**3
* + six*five*f6*term**4
C - I4(12)
nI412 = indxInv4(1,2)
bi412 = aInv(nI412)
term = zeta(1)*(bi412-zeta(1))
ua(2) = ua(2)
* + g2*term**2 + g3*term**3
* + g4*term**4 + g5*term**5
* + g6*term**6
ui1(nI412) = zeta(1) * (
* two*g2*term
* + three*g3*term**2
* + four*g4*term**3
* + five*g5*term**4
* + six*g6*term**5 )
ui2(indx(nI412,nI412)) = zeta(1)**2 * (
* two*g2
* + three*two*g3*term
* + four*three*g4*term**2
* + five*four*g5*term**3
* + six*five*g6*term**4 )
C
C Add volumetric energy
C
term = aInv(3) - one
ua(1) = ua(2) + dInv*term*term
C
return
end
C
C Maps index from Square to Triangular storage of symmetric
C matrix
C
integer function indx( i, j )
C
include 'aba_param.inc'
C
ii = min(i,j)
jj = max(i,j)
C
indx = ii + jj*(jj-1)/2
C
return
end
C
C
C Generate enumeration of Anisotropic Pseudo Invariants of
C type 4
C
integer function indxInv4( i, j )
C
include 'aba_param.inc'
C
ii = min(i,j)
jj = max(i,j)
C
indxInv4 = 4 + jj*(jj-1) + 2*(ii-1)
C
return
end
C
C
C Generate enumeration of Anisotropic Pseudo Invariants of
C type 5
C
integer function indxInv5( i, j )
C
include 'aba_param.inc'
C
ii = min(i,j)
jj = max(i,j)
C
indxInv5 = 5 + jj*(jj-1) + 2*(ii-1)
C
return
end