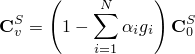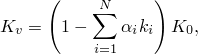4.8.2 Finite-strain viscoelasticity

Products: Abaqus/Standard Abaqus/Explicit

The finite-strain viscoelasticity theory implemented in Abaqus is a time domain generalization of either the hyperelastic or the hyperfoam constitutive models.

Integral formulation

It is assumed that the instantaneous response of the material follows from the hyperelastic constitutive equations:

for a compressible material and

for an incompressible material. In the above,

and

are, respectively, the deviatoric and the hydrostatic parts of the instantaneous Kirchhoff stress

is the “distortion gradient” related to the deformation gradient

where

is the volume change.

Using integration by parts and a variable transformation, the basic hereditary integral formulation for linear isotropic viscoelasticity can be written in the form

or entirely in terms of stress quantities,

where

is the reduced time,

, and

and

are the instantaneous small-strain shear and bulk moduli, and

and

are the time-dependent small-strain shear and bulk relaxation moduli. Recall that the reduced time represents a shift in time with temperature and is related to the actual time through the differential equation

where

is the temperature and

is the shift function.

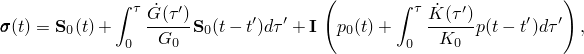
Using the volumetric/deviatoric-split hereditary integral in the reference configuration for large strain (hyperelastic) materials, and then using a standard push-forward operator (see Simo, 1987), one obtains the following set of equations in the current configuration:

where

and

is the distortional deformation gradient of the state at

relative to the state at t . A transformation is performed on the stress relating the state at time

to the state at time t.

Implementation

As in small-strain viscoelasticity, we represent the relaxation moduli in terms of the Prony series

where

and

are the relative moduli of terms i. Note that

. Abaqus assumes that the relaxation times

are the same so that from here on, we will sum on N terms for both bulk and shear behavior. In reality, the number of nonzero terms in bulk and shear,

and

, need not be equal, unless the instantaneous behavior is based on the hyperfoam model. In the latter case, the two deformation modes are closely related and are then assumed to relax equally and simultaneously.

Substituting Equation 4.8.2–2 and Equation 4.8.2–3 in Equation 4.8.2–1, we obtain

Next, we introduce the internal stresses, associated with each term of the series

These stresses are stored at each material point and are integrated forward in time. We will assume that the solution is known at time t, and we need to construct the solution at time

Integration of the hydrostatic stress

The internal hydrostatic stresses at time follow from

With

and

, it follows that

which yields with Equation 4.8.2–6

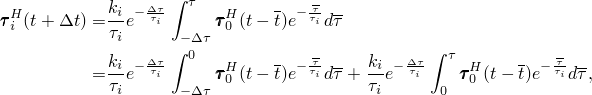
To integrate the first integral in Equation 4.8.2–7, we assume that varies linearly with the reduced time over the increment

Substituting into Equation 4.8.2–7 yields

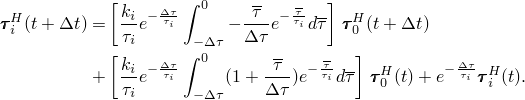
The integrals are readily evaluated, providing the solution at the end of the increment

or, in a slightly different form

with

Observe that for

and

. For

and

Integration of the deviatoric stress

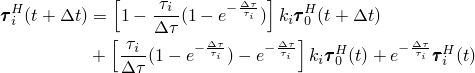
The internal deviatoric stresses at time follow from

Observe that

and the inverse of this is

which—when substituted into Equation 4.8.2–10, with

and

—gives

With

and

, it follows:

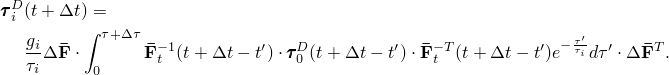
Now introduce the variable

Note that

and

Then we can also introduce

Substitution of Equation 4.8.2–5, Equation 4.8.2–12, and Equation 4.8.2–15 into Equation 4.8.2–11 yields

To integrate the first integral in Equation 4.8.2–16, we assume that varies linearly with the reduced time over the increment:

which with Equation 4.8.2–14 becomes

Equation 4.8.2–16 and Equation 4.8.2–17 for the deviatoric stress have exactly the same form as Equation 4.8.2–7 and Equation 4.8.2–8 for the hydrostatic stress. Hence, after integration we obtain

with

Equation 4.8.2–13, Equation 4.8.2–15, and Equation 4.8.2–18, thus, provide a straightforward integration scheme.

The total stress at the end of the increment becomes

which with Equation 4.8.2–9 and Equation 4.8.2–18 can also be written as

Rate equation

To solve the system of nonlinear equations generated by the constitutive equations, we need to generate the corotational constitutive rate equations. From Equation 4.8.2–20 it follows

where

is the corotational (Jaumann) stress rate. The rate form of the above equation is used to compute the Jacobian.

Cauchy versus Kirchhoff stress

All equations have been worked out in terms of the Kirchhoff stress. However, the implementation in Abaqus uses the Cauchy stress. To transform to Cauchy stress, we use the relations

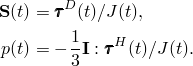
With , this allows us to write Equation 4.8.2–9, Equation 4.8.2–13, Equation 4.8.2–15, Equation 4.8.2–18, and Equation 4.8.2–19 in the following form:

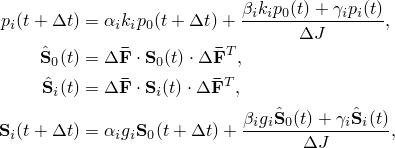
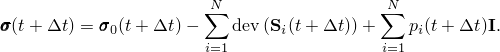
The virtual work and rate of virtual work equations are written with respect to the current volume. Therefore, the corotational stress rates are rates of Kirchhoff stress mapped into the current configuration and transformed in the same way as the stresses themselves.

This set of equations—combined with the expressions for , , and —describe the full implementation of the hyper-viscoelasticity model in a displacement formulation.