Abaqus/Standard offers a “subspace” steady-state dynamic analysis procedure for structures subjected to continuous harmonic excitation.

Abaqus/Standard also offers a “modal” procedure described in “Steady-state linear dynamic analysis,” Section 2.5.7 and a “direct” procedure described in “Direct steady-state dynamic analysis,” Section 2.6.1.

The “subspace” steady-state dynamic analysis procedure is activated by defining a subspace-based steady-state dynamic analysis step. This procedure is a perturbation procedure, where the perturbed solution is obtained by linearization about the current base state. For the calculation of the base state the structure may exhibit material and geometrical nonlinear behavior as well as contact nonlinearities. Structural and viscous damping can be included in the procedure using the Rayleigh and structural damping coefficients specified under the material definition. The procedure can also be used for viscoelastic material modeling (“Frequency domain viscoelasticity,” Section 4.8.3). Discrete damping such as mass, dashpots, spring, and connector elements can be included. The main advantage of this method is that it allows frequency-dependent behavior to be considered at a relatively small cost increase over the purely linear analysis via the “modal” procedure described in “Steady-state linear dynamic analysis,” Section 2.5.7.

The discretized form of the linearized dynamic virtual work equation for a solid or structural system can be written as

where the following definitions apply: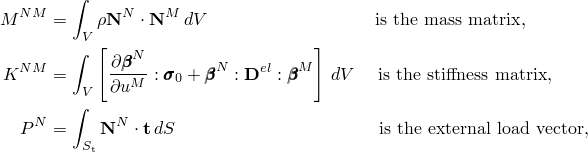 is the viscous damping matrix, is the imaginary stiffness proportional damping matrix representing a structural damping matrix, and are the velocity and the acceleration, is the density of the material, is the stress in the base state, is the surface traction, and is the elasticity matrix for the material. We assume that both the stiffness and the damping are frequency dependent.

For acoustic media, similar equations apply (see “Coupled acoustic-structural medium analysis,” Section 2.9.1):

The “structural damping” operator in this acoustic case is defined as the extension of structural damping to the acoustic matrices:that is, the acoustic stiffness matrix times a constant. The acoustic “structural damping” operator inherits the frequency dependence of the acoustic stiffness matrix caused by volumetric drag.

The eigenfrequency step prior to the subspace-based steady-state dynamic analysis has extracted eigenmodes of the undamped system using

where is the eigenfrequency in radians/time. The procedure assumes that the complex displacement changes for the damped system can be written in the form where are the complex modal amplitudes. Using Equation 2.6.2–3 in Equation 2.6.2–1 and premultiplying with , the equation of motion projected onto the subspace is provided:where and is the excitation frequency. Since the eigenmodes are not orthogonal to the damping and stiffness matrices in the equilibrium equations (because of the frequency-dependent properties), the projected damping and stiffness matrices are not diagonal.

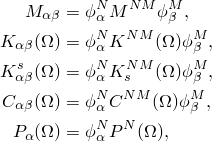
For harmonic excitation and response we can write

where and are the real and imaginary parts of the modal amplitudes and and are the real and imaginary parts of the amplitude of the force applied to the structure after projection onto the subspace. Substituting the expressions for harmonic excitation and response in Equation 2.6.2–4 and writing the result in matrix form yieldswhere

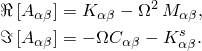
The equation is solved for the real and imaginary part of the complex modal amplitudes , and Equation 2.6.2–3 can be used to compute the real and imaginary part of the nodal displacements.

For a coupled acoustic-structural analysis the development is similar. However, in this case the “damping” matrix also contains volumetric drag, impedance boundary, radiating boundary, and fluid-solid coupling effects. Although the original formulation of the coupled acoustic-structural eigenvalue extraction problem is unsymmetric, the equations are rearranged such that the fluid-solid coupling effects are retained without making the problem unsymmetric. The resulting modes and frequencies are associated with the coupled, undamped fluid-solid system. The subspace-based steady-state dynamic procedure will project the full, coupled, and damped acoustic-structural system of equations onto the space spanned by the set of coupled fluid-solid modes.

For an acoustic-only analysis the development is very similar to that of the solid-only case. The acoustic material damping equivalent, volumetric drag, is treated in a similar manner to solid material damping effects.