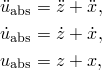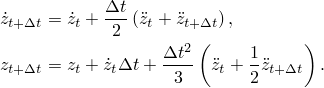Abaqus Theory Guide  


2.5.5 Modal dynamic analysis

Product: Abaqus/Standard  

The modal dynamic procedure provides time history analysis of linear systems.

The excitation is given as a function of time: it is assumed that the amplitude curve is specified so that the magnitude of the excitation varies linearly within each increment. When the model is projected onto the eigenmodes used for its dynamic representation, we obtain the following set of equations at time t:

where the and indices span the eigenspace; is the projected viscous damping matix; is the “generalized coordinate” of the mode (the amplitude of the response in this mode); is the natural frequency of the undamped mode (obtained as the square root of the eigenvalue in the eigenfrequency step that precedes the modal dynamic time history analysis);  is the magnitude of the loading projected onto this mode (the “generalized load” for the mode); and is the change in f over the time increment, which is .

If the projected damping matrix is diagonal, Equation 2.5.5–1 becomes the following uncoupled set of equations:

where is the critical damping ratio given by the relation

where is the modal viscous damping coefficient and is the modal mass in mode .

Solution to the uncoupled system

The solution to the uncoupled equations is obtained readily as a particular integral for the loading and a solution to the homogeneous equation (with no right-hand side). These solutions can be combined and written in the general form

where and , are constants, since we have assumed that the loading only varies linearly over the time increment (that is, is constant).

There are three cases of this solution for nonrigid body motion (), depending on whether the damping in the modal equilibrium equation is greater than, equal to, or less than critical damping (that is, depending on whether is positive, zero, or negative).

Solution to the coupled system

Equation 2.5.5–3 can be generalized to address full coupling in the projected damping matrix. Let the matrix be split into its diagonal and off-diagonal parts so that

Then, with the additional assumption that the off-diagonal damping force varies linearly over a time increment, the equation for the uncoupled system can be rewritten as

where is given by

is fully populated but is a function only of , so it needs to be factored only a single time for a given analysis.

Integral coefficients

There are three cases of this solution for nonrigid body motion (), depending on whether the damping in the modal equilibrium equation is greater than, equal to, or less than critical damping (that is, depending on whether is positive, zero, or negative).

Damping less than critical

This case is the most common. With

we have

Damping equal to critical

In this case

Damping higher than critical

In this case, with

we have

Rigid body mode with damping

If there are rigid body modes in the finite element model, there will be one or several eigenvalues that are zero. The equation of motion (Equation 2.5.5–1) is reduced to

Only Rayleigh damping can be specified for a rigid body mode, since the critical damping is zero. Furthermore, since it is a rigid body mode, only the mass damping factor, , appears (stiffness damping requires that there be straining of the body). For this case

Rigid body mode without damping

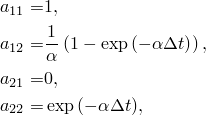
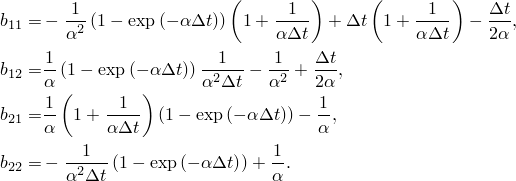
For the particular case of a rigid body mode without damping, the equation of motion (Equation 2.5.5–1) is reduced to

For this case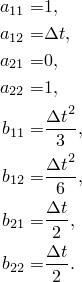

Structural damping in modal dynamic analysis

Structural damping is a commonly used damping model that represents damping as complex stiffness. This representation causes no difficulty for frequency domain analysis such as steady-state dynamics for which the solution is already complex. However, in the time domain, the solution must remain real-valued. To allow users to apply their structural damping model in the time domain, a method has been developed to convert structural damping to an equivalent viscous damping. This technique was designed so that, in the frequency domain, the viscous damping applied is identical to structural damping if the projected damping matrix is diagonal.

We start with the equation of a single degree-of-freedom oscillator,

where m is the mass, c is the viscous damping factor, k is the stiffness, x is the response, f is the force, and is the structural damping factor. If we normalize by the mass and assume harmonic input, we obtain the relation

where is the natural frequency, is the excitation frequency, is the coefficient of the harmonic response, and is the coefficient of the harmonic input. The relation between the viscous damping factor c and the critical damping factor is such that .

Based on the two previous equations, if we want the viscous damping factor to have the same effect as the structural damping factor, we must have

If we further assume that , the relation simplifies to

Now we consider the finite element system of equations,

where is the finite element viscous damping matrix and is the finite element structural damping matrix. If we project these equations onto the eigenmodes, the damping matrices become

which could be fully populated. If we take the case that and are diagonal, their diagonal elements can be written

where is a particular mode. Maintaining the relation developed for the single degree-of-freedom system for this diagonal case would require

For nondiagonal matrices the expression for equivalent viscous damping becomes

where D is a diagonal matrix whose entries are given by

Response of nodal and element variables

The time integration is done in terms of the generalized coordinates, and the response of the physical variables is then immediately available by summation:

where are the modes, are the modal strain amplitudes, are the modal stress amplitudes, and are the modal reaction force amplitudes corresponding to each eigenvector .

Initial conditions

At the beginning of the step initial displacements and initial velocities must be converted to equivalent values of the generalized coordinates, which can be done exactly only if the number of eigenvectors equals the number of degrees of freedom. Since this is usually not the case, the initial values of the generalized coordinate displacement and velocity are calculated as

where is the generalized mass for the eigenvector , is the eigenvector, is the mass matrix, and are the initial displacements.

Similarly, for the initial velocities

For the case where the initial conditions are given by a previous modal dynamic analysis, the generalized displacement, velocity, and acceleration are simply taken from the previous analysis.

Base motion definition

Many linear dynamic problems involve finding the response of a structure to a “base motion”: a time history of displacement, velocity, or acceleration given for the points where the displacements of the structure are prescribed. In all cases these base motions are converted into an acceleration history. If the displacement or velocity history has nonzero values at time 0, corrections to the acceleration histories are made at times 0 and . If velocities are given, the acceleration at 0 is

If displacements are given, the accelerations at 0 and are

In the above expressions and in the expressions to follow, a superscript * indicates user-defined amplitude data.

If velocities are given for tabular or equally spaced amplitude curve definitions, the acceleration is defined by the central difference rule

If displacements are given, the acceleration is defined by the central difference rule

The response is calculated relative to the base. If total values of nodal variables are required, the motion at the base is added to the relative values:

where

Reference