
Product: Abaqus/Standard
Benefits: New functionality provides better accuracy of and robustness for implicit simulations involving interactions modeled with general contact.
Description: Simulations using general contact submitted from 3DEXPERIENCE platform Scenario Creation apps can use a new technique to improve finite element representations of contact surfaces. This technique has some similarity to existing circumferential, spherical, and toroidal smoothing methods in Abaqus because the contact geometry corrections are based on deviations of the original element-based surface geometry from a more accurate reference representation of the undeformed geometry. The new technique leverages CAD surface representations available in the 3DEXPERIENCE platform in the computation of contact geometry corrections. This technique is not available in explicit dynamic steps.
The CAD-based smoothing method is applicable to arbitrary surface shapes having CAD representations in the 3DEXPERIENCE platform. Consider the example shown in Figure 10–1. This example is constructed such that the analytical solution has a uniform, uniaxial stress state of 108 Pa. The curved contact interface has closed contact and sticking friction everywhere, and the same elastic material exists on both sides of the contact interface. The meshes used in this example are made of quadratic hexahedral and wedge elements. The meshes do not have matched nodes across the contact interface, which causes significant stress noise, especially for small strains where the level of element deformation is less than or equal to the distances associated with the mismatch of faceted surface representations across the interface.
Figure 10–1 Two solid blocks contacting on an arbitrarily curved interface (subjected to uniform unidirectional compressive stress).

Figure 10–2 shows that CAD-enhanced contact reduces stress noise for this example. For example, the maximum Mises stress deviates from the analytical Mises stress solution by 33% without CAD-enhanced contact, and this deviation is less than 3% with CAD-enhanced contact.
Figure 10–2 Comparison of the Mises stress field between the case without geometry-based corrections (left) and with geometry-based corrections applied to the curved contacting surfaces (right).
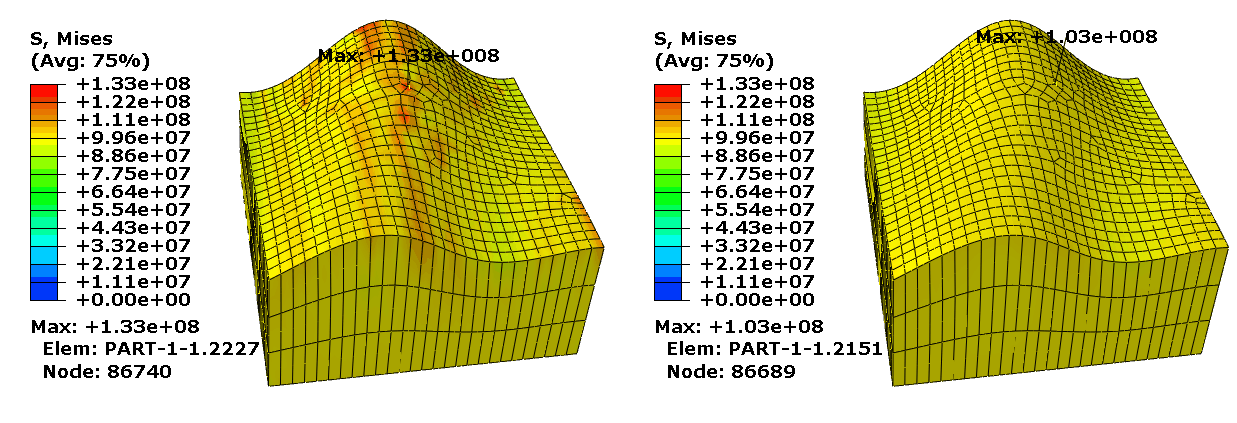
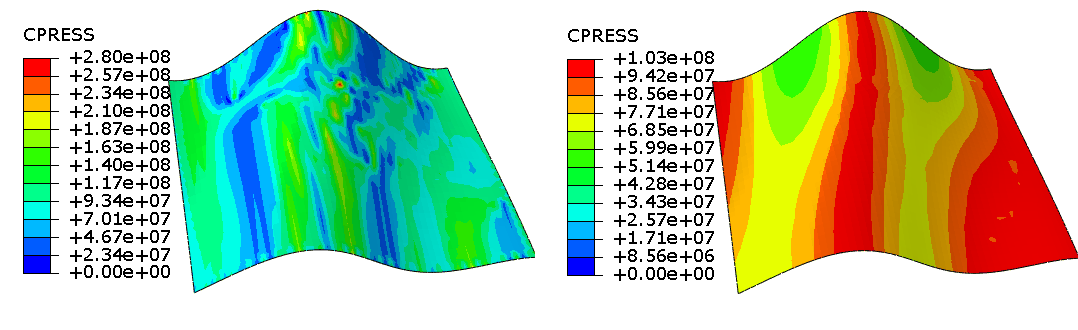
Figure 10–3 compares contact pressure solutions for this example with and without CAD-enhanced contact. CAD-enhanced contact greatly reduces the contact pressure noise in this example. The contact pressure is not expected to be uniform in this example: the analytical solution of traction at a given location on the contact interface is equal to the uniaxial stress tensor contracted with the local surface normal direction, and the normal direction varies over the surface.
Figure 10–3 Contact pressure field without geometry-based corrections (left) compared to the case when geometry-based corrections are applied to the curved contacting surfaces (right).
The effects of this smoothing approach tend to be most significant for analyses involving small deformation and coarse mesh discretization with first-order elements in the contact region; however, significant benefits are common even when the mesh is quite refined or higher-order elements are used. This smoothing technique often has an insignificant effect on solutions after large deformation if the geometry-correction distances are small compared to the element dimensions. However, the smoothing can degrade the solution accuracy after large deformation in some cases. The effectiveness of surface-to-surface contact smoothing does not degrade upon relative motion between the contact surfaces; for example, the smoothing technique works well for cases involving large sliding but small deformation.
This method will not overcome all robustness and accuracy issues associated with a coarse mesh. For example, resolving complex stress variations requires adequate mesh refinement even when a CAD-based (or other) surface smoothing approach is used. Use of extremely coarse meshes at curved contact interfaces will still tend to degrade simulation robustness.
References: